Understanding the ln graph is essential for anyone delving into the world of mathematics, particularly in the field of logarithmic functions. This graph represents the natural logarithm function, which plays a critical role in various scientific and engineering applications. Whether you are a student seeking to comprehend the concept or a professional looking to apply logarithmic principles in your work, mastering the ln graph is crucial. By visualizing and interpreting the ln graph, one can gain insights into the behavior of logarithmic functions and their practical implications.

The ln graph is characterized by its distinct shape, which reflects the nature of the natural logarithm. As the input values increase, the output values approach infinity, but at a decreasing rate. This unique property makes the ln graph a fascinating topic for exploration and analysis. Understanding its features, such as intercepts, asymptotes, and increasing or decreasing trends, can enhance your grasp of logarithmic functions and their applications in real-world scenarios.

In this article, we will navigate through the intricacies of the ln graph, uncovering its fundamental aspects and applications. We will address common questions related to this graph, clarify its significance in mathematics, and provide practical examples that illustrate its use. Join us in this exploration of the ln graph, where we will unlock the secrets of logarithmic functions and discover their importance in various fields.

What is the ln Graph?

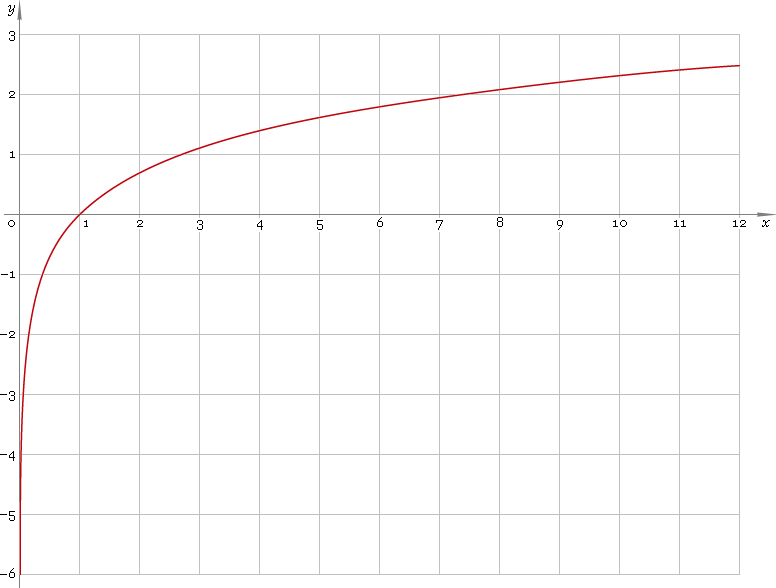
The ln graph represents the natural logarithm function, denoted as ln(x). It is defined for positive real numbers, and its output is the power to which the base 'e' (approximately 2.718) must be raised to obtain the input value x. The ln graph showcases the relationship between the input x and the output ln(x), making it a vital tool in both theoretical and applied mathematics.

How is the ln Graph Constructed?

Creating an ln graph involves plotting points corresponding to various x values and their respective ln(x) outputs. Here are the steps to construct the ln graph:

Choose a range of positive x values (e.g., 0.1, 1, 2, 3, etc.).
Calculate the natural logarithm for each x value using a scientific calculator or logarithmic table.
Plot the points on a Cartesian coordinate system, with x on the horizontal axis and ln(x) on the vertical axis.
Connect the points to form a smooth curve, which represents the ln graph.

What Are the Key Features of the ln Graph?

The ln graph possesses several noteworthy characteristics:

Intercept: The ln graph intersects the x-axis at the point (1, 0), as ln(1) equals 0.
Asymptote: The graph approaches the vertical line x = 0 but never touches it, indicating that ln(x) approaches negative infinity as x approaches 0 from the right.
Increasing Function: The ln graph is an increasing function, meaning that as x increases, ln(x) also increases.
Concavity: The graph is concave down for all positive x values, reflecting a diminishing rate of increase.

What Are the Applications of the ln Graph?

The ln graph and the natural logarithm have numerous applications across various fields, including:

Mathematics: Used in calculus, particularly in integration and differentiation.
Physics: Helpful in solving problems related to exponential decay and growth.
Economics: Utilized in calculating compound interest and understanding economic models.
Biology: Important in population studies and understanding growth rates.

How Do You Interpret the ln Graph?

Interpreting the ln graph involves understanding the relationship between x and ln(x). Here are some key points to consider:

For x values between 0 and 1, ln(x) yields negative values, indicating that the function decreases.
At x = 1, the function reaches 0, marking a significant point on the graph.
For x values greater than 1, ln(x) increases, showing positive growth.

What Are Common Mistakes When Working with the ln Graph?

When working with the ln graph, individuals may encounter several common mistakes:

Assuming that ln(x) is defined for x ≤ 0; it is only defined for positive x values.
Misinterpreting the behavior of the graph near the vertical asymptote at x = 0.
Overlooking the rapid increase of ln(x) for larger x values, leading to underestimating the function's growth.

How Can You Practice Working with the ln Graph?

To become proficient in understanding and utilizing the ln graph, consider the following practice methods:

Plot various ln(x) points manually and observe the behavior of the graph.
Use graphing software or online graphing calculators to visualize the ln graph and experiment with different x values.
Engage in exercises that involve solving logarithmic equations and interpreting their graphical representation.

Can You Provide Examples of the ln Graph?

Here are a few examples to illustrate the ln graph:

Example 1: For x = 2, ln(2) ≈ 0.693, which corresponds to the point (2, 0.693) on the graph.
Example 2: For x = 3, ln(3) ≈ 1.099, representing the point (3, 1.099).
Example 3: For x = 0.5, ln(0.5) ≈ -0.693, illustrating the negative output for values between 0 and 1.

Conclusion: Why is the ln Graph Important?

In conclusion, the ln graph is a vital component of mathematics, offering insights into logarithmic functions and their applications across various fields. By understanding its features, interpretations, and practical uses, individuals can enhance their mathematical skills and apply logarithmic principles effectively. Whether for academic pursuits or professional applications, mastering the ln graph is a crucial step toward success in math and beyond.